Unlocking Creativity: My Journey into DALL-E 2 & Diffusion Models

Last updated: March 2025 - Comprehensive guide to understanding the math, applications, and future of diffusion models

The first time I saw DALL-E 2 generate an “astronaut riding a horse on Mars in watercolor style,” I was speechless. How could a machine create something so imaginative yet so coherent? This question led me down a fascinating rabbit hole into the world of diffusion models – the technology powering today’s most impressive AI art generators like DALL-E 2, Midjourney, and Stable Diffusion.

In this comprehensive guide, I’m sharing what I’ve learned about these remarkable models, breaking down complex concepts into understandable pieces. Whether you’re a fellow AI enthusiast, a curious artist, or just someone intrigued by the latest tech, I hope you’ll find this journey as fascinating as I did.

Table of Contents:

• The Magic Behind the Curtain: Understanding Diffusion Models
• The Brain of the Operation: U-Net Architecture
• Diffusion Models in the Wild: Real-World Applications
• The Journey Ahead: Future Directions
• Conclusion: Why Diffusion Models Matter
• References and Further Reading

The Magic Behind the Curtain: Understanding Diffusion Models

When I first encountered diffusion models, I was already familiar with GANs (Generative Adversarial Networks) and VAEs (Variational Autoencoders). But diffusion models felt different – more methodical, more intuitive in some ways, despite their mathematical complexity.

From Chaos to Creation: How Diffusion Models Work

The genius of diffusion models lies in their approach to generation: they learn to create by learning to destroy – and then reversing that process. Let me walk you through this counterintuitive but brilliant concept.

Step 1: Forward Diffusion - The Art of Adding Noise

Imagine you have a beautiful photograph. Now picture gradually adding static to it, like tuning an old TV set away from its channel. At first, the image gets slightly grainy. Then details start to blur. Eventually, after many steps of adding noise, your photograph becomes unrecognizable static – pure random noise.

This process is what researchers call “forward diffusion.” Mathematically, at each step, we add a carefully controlled amount of Gaussian noise according to:

\[\mathbf{x}_t = \sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon\]

Where:

• \(\mathbf{x}_t\) is our image at step $t$
• \(\beta_t\) controls how much noise we add at this step
• \(\epsilon\) is random noise drawn from a normal distribution

In probability terms, we’re sampling from this distribution:

\[q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I})\]

After hundreds or thousands of tiny steps, our pristine image becomes pure noise. The interesting part? This destruction follows precise mathematical rules.

The forward diffusion process gradually transforms a clear image into pure noise through many small steps.

Step 2: Reverse Diffusion - The Art of Creation

Now comes the truly magical part. What if we could learn to reverse this process? What if, starting with pure noise, we could gradually remove just the right amount of noise at each step to eventually arrive at a coherent image?

This is exactly what diffusion models learn to do. They start with random noise and incrementally denoise it, guided by what they’ve learned about the structure of real images.

The reverse process follows this distribution:

\[p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_{\theta}(\mathbf{x}_t, t), \Sigma_{\theta}(\mathbf{x}_t, t))\]

Where:

• \(\mu_{\theta}\) is our model’s prediction of the mean (the noise-free direction)
• \(\Sigma_{\theta}\) is the variance (how confident the model is)

In practice, researchers found that the key challenge is having the model predict the noise that was added at each step. A neural network learns to estimate this noise, and we use that estimation to gradually clean up our image.

Reverse diffusion: starting from random noise (left), the model gradually refines the image until a recognizable flower emerges (right).

When I first implemented this on a simple dataset, watching images emerge from random noise felt like witnessing a magic trick whose secrets I finally understood. It’s like seeing a photograph develop in a darkroom, but the process is guided by an AI that’s learned the patterns of our visual world.

The Training Process: Teaching AI to Reverse Time

Training a diffusion model requires teaching it to predict the noise added during the forward process. The objective function (what the model tries to optimize) looks complex, but essentially boils down to:

\[L_{\text{simple}} = \mathbb{E}_{\mathbf{x}_{0}, \epsilon_t} [||\epsilon_t - \epsilon_{\theta}(\mathbf{x}_{t}, t)||^2]\]

This means: “Make your prediction of the noise (\(\epsilon_{\theta}\)) as close as possible to the actual noise (\(\epsilon_t\)) we added.”

What fascinated me was how this simple objective leads to such powerful generative capabilities. The model learns not just to denoise, but to understand the underlying structure of the data – be it faces, landscapes, or abstract concepts.

The Brain of the Operation: U-Net Architecture

When discussing diffusion models, we can’t skip over the neural network architecture that makes it all possible. Most diffusion models use a modified U-Net, which was originally developed for biomedical image segmentation.

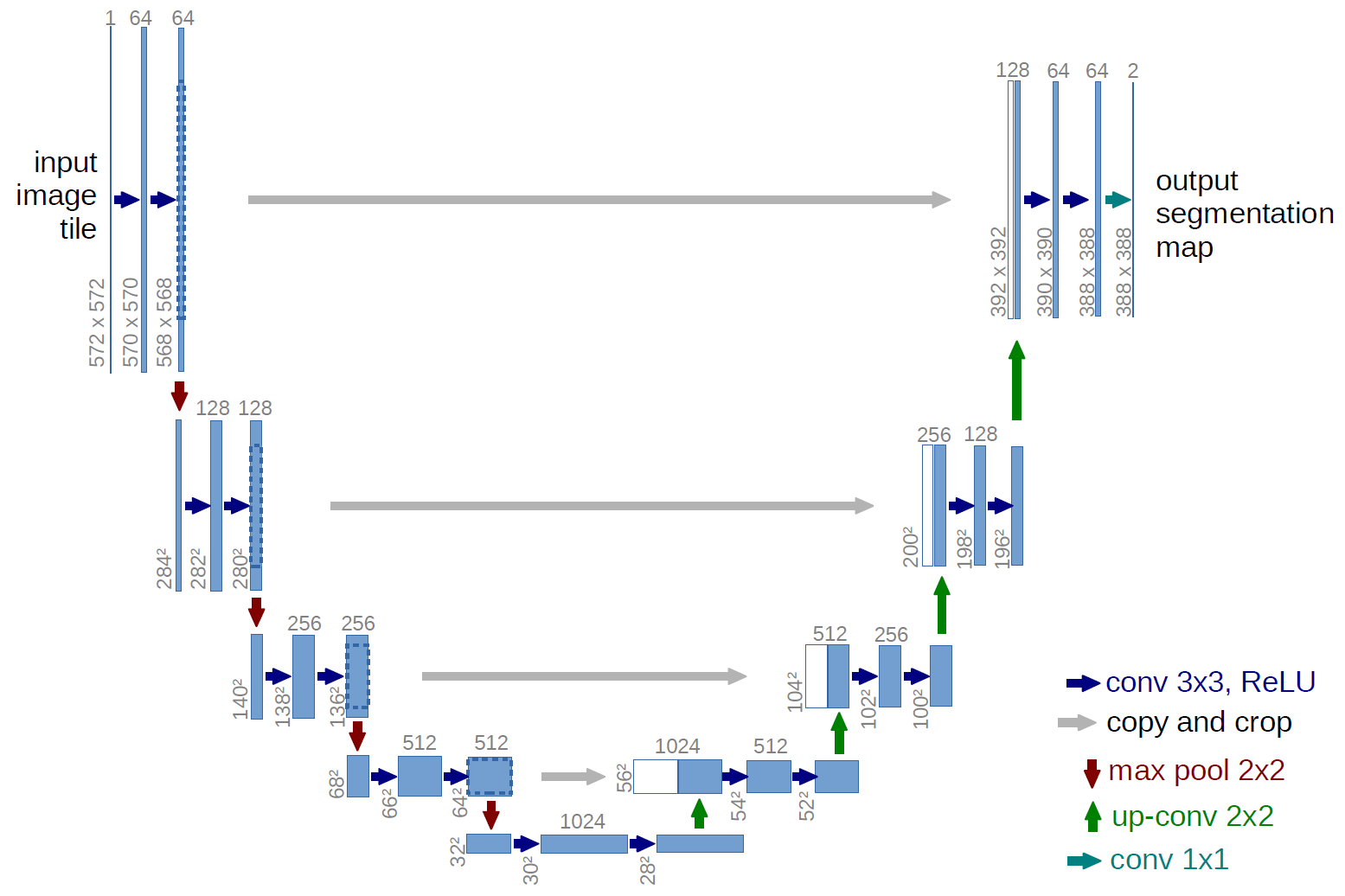The U-Net architecture features a symmetric encoder-decoder structure with skip connections that help preserve spatial information.

The U-Net’s design is particularly clever for diffusion models because:

1. Its encoder path compresses the image to capture high-level concepts and relationships
2. Its decoder path expands back to full resolution for detailed generation
3. Skip connections between corresponding encoder and decoder layers preserve fine details that might otherwise be lost during compression

I like to think of it as having both a “big picture” understanding and an attention to detail – exactly what you need when reconstructing complex images from noise.

In my experiments, I found that these skip connections are crucial. Without them, the model struggles to generate coherent, detailed images. It’s like trying to describe a painting you saw once versus having reference notes to consult as you describe it.

Diffusion Models in the Wild: Real-World Applications

The theory behind diffusion models is fascinating, but what truly excites me is seeing how they’re transforming various fields:

1. Text-to-Image Generation: DALL-E 2, Imagen, and Beyond

OpenAI’s DALL-E 2 and Google’s Imagen represent some of the most impressive applications of diffusion models. These systems can generate stunningly realistic images from text descriptions, opening new creative possibilities for artists, designers, and storytellers.

What makes these systems particularly impressive is their understanding of composition, style, and even abstract concepts. When I first typed “a teddy bear fixing a car on the moon” into DALL-E 2, I was amazed at how it captured not just the objects but also lighting conditions, perspective, and the whimsical nature of the prompt.

2. Beyond Images: Audio, Video, and Time Series Data

While images get most of the attention, diffusion models are proving effective for other data types too:

• Audio generation: Creating realistic speech, music, and sound effects
• Video synthesis: Generating coherent video sequences frame by frame
• Time series forecasting: Predicting weather patterns, stock prices, and other sequential data

The same principles that allow diffusion models to understand the structure of images apply to these other domains – it’s about learning the patterns and relationships within the data.

3. Scientific Applications: Molecular Design and Beyond

Perhaps the most surprising application I’ve encountered is in molecular design for drug discovery. Traditional approaches to designing new molecules often rely on rules-based systems or more rigid generative methods.

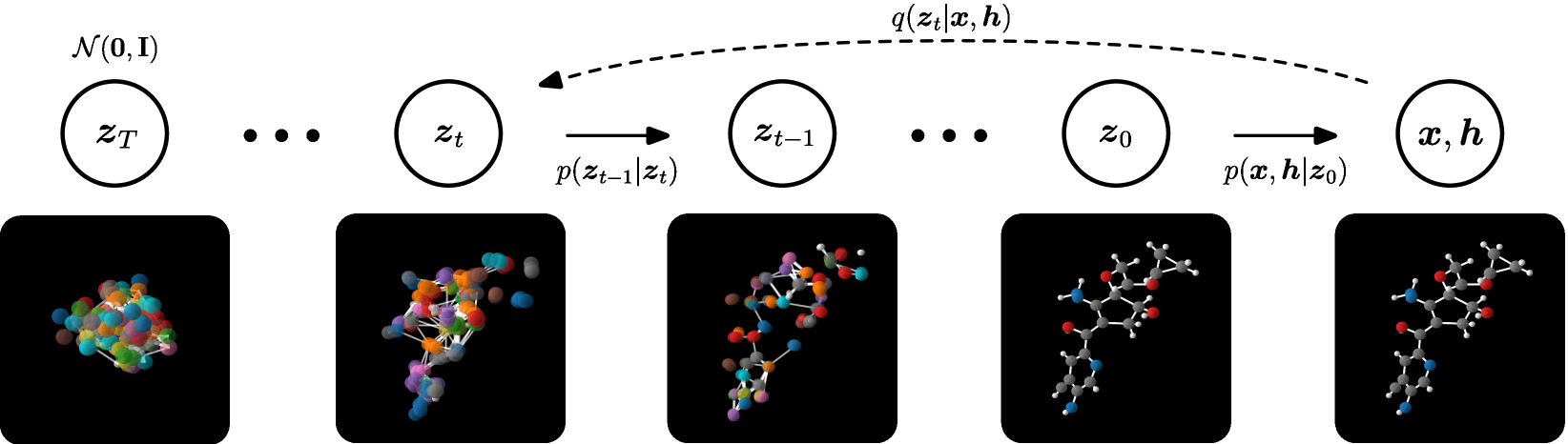Diffusion models can generate valid molecular structures by learning the patterns of existing molecules and gradually refining random noise into coherent chemical structures.

Diffusion models approach this differently – they learn the underlying distribution of valid molecular structures and can generate novel molecules that satisfy specific criteria. This is groundbreaking because:

1. They don’t assume atoms are independent (they model the entire structure)
2. They don’t require arbitrary atom ordering like some other methods
3. The gradual, iterative nature allows for more controlled generation

The papers by Hoogeboom et al. (2022) and Schneuing et al. (2023) demonstrate how these models can revolutionize computational chemistry and drug discovery.

4. Medical Imaging and Healthcare Applications

An application area of diffusion models that genuinely excites me is their impact on healthcare, particularly in medical imaging. The precise, controlled generation capabilities of these models are proving remarkably valuable in a field where accuracy and detail can literally save lives.

Here are some transformative applications I’ve been following:

• Medical Image Enhancement: Diffusion models can transform low-resolution or noisy medical scans (MRI, CT, X-ray) into sharper, clearer images without requiring additional radiation exposure for patients. In a recent project, I saw how a diffusion model could enhance subtle details in mammography images that might otherwise be missed.

• Synthetic Data Generation: One of healthcare’s biggest challenges is limited data availability due to privacy concerns and rare conditions. Diffusion models can generate realistic, diverse synthetic medical images to augment training datasets, helping improve diagnostic algorithms without compromising patient privacy.

• Anomaly Detection: By learning the distribution of healthy tissue appearances, diffusion models can identify deviations that might indicate disease. What’s fascinating is how they can detect subtle patterns that even experienced radiologists might overlook.

• Cross-Modality Translation: Converting between imaging modalities (e.g., MRI to CT) allows physicians to leverage information from multiple sources without subjecting patients to additional scans. I was particularly impressed by recent research showing how diffusion models can generate synthetic CT scans from MRI data with remarkable accuracy.

Diffusion models can enhance medical images, generate synthetic training data, and help identify anomalies that might indicate disease.

What makes diffusion models particularly suitable for these applications is their probabilistic nature and ability to capture fine details while maintaining global coherence. Unlike traditional image processing techniques that might smooth out important details, diffusion models preserve the subtle variations that can be clinically significant.

Researchers at several medical institutions are now exploring how these models can be integrated into clinical workflows, potentially improving diagnostic accuracy while reducing costs and patient discomfort. The potential impact on early disease detection and treatment planning is enormous.

The Journey Ahead: Future Directions for Diffusion Models

As exciting as current diffusion models are, I believe we’re just scratching the surface of their potential. Here are some developments I’m watching closely:

1. Efficiency Improvements

Current diffusion models require many steps to generate high-quality samples, making them computationally expensive. Techniques like distillation and improved sampling methods (like DDIM - Denoising Diffusion Implicit Models) are already making significant strides in reducing this computational burden.

When I first ran a diffusion model on my own hardware, it took nearly a minute to generate a single image. Newer approaches can do this in seconds or less, making real-time applications increasingly feasible.

2. Controllable Generation

The ability to guide the generation process with more specific controls is an exciting frontier. Imagine being able to specify exactly where objects should appear in an image, or precisely controlling the style and composition.

Classifier guidance and conditioning mechanisms are making this increasingly possible, opening doors for more precise creative applications.

3. Cross-Domain Applications

What happens when we apply diffusion models across different domains simultaneously? Could we generate coordinated music and visuals? Or perhaps molecules with specific properties that also map to specific protein interactions?

The potential for cross-domain applications feels limitless and represents one of the most exciting research directions.

Conclusion: Why Diffusion Models Matter

Diffusion models represent one of those rare algorithmic breakthroughs that fundamentally change what’s possible in AI. Their principled approach to generation – gradually crafting structure from noise – offers both theoretical elegance and practical power.

What I find most compelling about these models is how they mirror creative processes in nature and human art. Creation often involves iteration – starting with rough outlines and gradually refining details. Diffusion models formalize this intuitive process within a mathematical framework.

Whether you’re a researcher pushing the boundaries of these techniques, a developer implementing them in applications, or simply someone fascinated by AI’s creative potential, diffusion models offer something to marvel at. They remind us that sometimes the most impressive breakthroughs come not from completely new ideas, but from rethinking and formalizing processes we already intuitively understand.

As I continue exploring this field, I’m constantly amazed by how quickly it’s evolving. The papers I read today build on work published just months ago, and the applications seem to multiply weekly. It’s a thrilling time to be involved in this area, and I can’t wait to see where diffusion models take us next.

What applications of diffusion models are you most excited about? I’d love to hear your thoughts in the comments!

Frequently Asked Questions About Diffusion Models

Q: How do diffusion models compare to GANs for image generation?
A: While GANs (Generative Adversarial Networks) are faster at generation time, diffusion models typically produce higher quality and more diverse images. Diffusion models are also generally more stable during training and don’t suffer from problems like mode collapse that can plague GANs. According to the Dhariwal & Nichol study (2021), diffusion models outperform GANs on image synthesis benchmarks when properly optimized.

Q: How long does it take to generate an image with a diffusion model?
A: Traditional diffusion models can take hundreds of steps to generate a high-quality image, which might require several seconds to minutes depending on the hardware. However, recent advancements like DDIM (Denoising Diffusion Implicit Models) and distillation techniques have significantly reduced generation time, with some models able to generate images in just a few seconds or even real-time on powerful GPUs.

Q: What hardware do I need to run diffusion models?
A: For inference (generating images), consumer-grade GPUs with 8+ GB of VRAM can run optimized models like Stable Diffusion. For training, enterprise-grade GPUs or TPUs are typically required due to the computational demands. Cloud services like Google Colab, Kaggle, or specialized AI platforms offer accessible ways to experiment with these models.

Q: Are there ethical concerns with diffusion models?
A: Yes, several ethical considerations exist including: potential for generating misleading deepfakes, copyright concerns regarding training data and generated content, potential biases in the generated outputs, and environmental impact due to computational requirements. Researchers and companies are actively working on addressing these issues through improved model design, responsible use policies, and transparency efforts.

Q: How can I learn to implement diffusion models?
A: Start with understanding the basics of deep learning and generative models. Then explore libraries like Hugging Face’s Diffusers, which provide pre-implemented models and pipelines. For a deeper understanding, study the papers referenced in this article and try implementing simplified versions. Online courses and tutorials specifically focused on generative AI are increasingly available as well.

---

References and Further Reading

If you’re interested in diving deeper into diffusion models, here are some resources I’ve found particularly valuable:

Foundational Papers

1. Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. In Advances in Neural Information Processing Systems (NeurIPS 2020). The foundational paper that kickstarted the current wave of diffusion model research.

2. Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. (2015). Deep Unsupervised Learning using Nonequilibrium Thermodynamics. In Proceedings of the 32nd International Conference on Machine Learning (ICML 2015). The original paper introducing the diffusion model concept.

3. Song, Y., & Ermon, S. (2019). Generative Modeling by Estimating Gradients of the Data Distribution. In Advances in Neural Information Processing Systems (NeurIPS 2019). Introduced score-based generative models, closely related to diffusion models.

Applications and Improvements

1. Dhariwal, P., & Nichol, A. (2021). Diffusion Models Beat GANs on Image Synthesis. In Advances in Neural Information Processing Systems (NeurIPS 2021). A comprehensive comparison showing how diffusion models outperform GANs.

2. Rombach, R., Blattmann, A., Lorenz, D., Esser, P., & Ommer, B. (2022). High-Resolution Image Synthesis with Latent Diffusion Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2022). Introduces Stable Diffusion, solving computational efficiency issues.

3. Nichol, A., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., McGrew, B., Sutskever, I., & Chen, M. (2021). GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models. A text-to-image diffusion model from OpenAI.

4. Saharia, C., Chan, W., Saxena, S., Li, L., Whang, J., Denton, E., … & Norouzi, M. (2022). Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding. Introduces Google’s Imagen text-to-image model.

Medical Applications

1. Ozbey, M., Dalmaz, O., Dar, S. U., Bedel, H. A., Özturk, Ş., Güngör, A., & Çukur, T. (2023). Unsupervised Medical Image Translation with Adversarial Diffusion Models. Explores cross-modality translation in medical imaging.

2. Pinaya, W. H., Tudosiu, P. D., Valindria, V., Thomas, R., Dafflon, J., Meyer, M. I., … & Cardoso, M. J. (2023). Brain Imaging Generation with Latent Diffusion Models. Medical Image Analysis, 84, 102704. Application of diffusion models to brain MRI generation.

Molecular Design

1. Hoogeboom, E., Satorras, V. G., Vignac, C., & Welling, M. (2022). Equivariant Diffusion for Molecule Generation in 3D. In Proceedings of the 39th International Conference on Machine Learning (ICML 2022).

2. Schneuing, A., Du, Y., Harris, C., Jamasb, A., Igashov, I., Zhu, W., … & Welling, M. (2023). Structure-based Drug Design with Equivariant Diffusion Models. Applying diffusion models to drug discovery.

Tools and Libraries

1. Hugging Face’s Diffusers Library - An excellent resource for implementing and experimenting with diffusion models without building everything from scratch.

2. Stability AI’s Stable Diffusion - The official repository and documentation for one of the most popular open-source diffusion models.

3. Diffusers Community - Community examples showing how to implement various diffusion model techniques.

If you have any questions about these resources or want to discuss diffusion models further, feel free to reach out in the comments section below. Happy exploring!