Imagine zooming into the fabric of spacetime itself, magnifying it by a factor of $10^{35}$—from human scales down to the Planck length of approximately $1.6 \times 10^{-35}$ meters. What would you see? According to Loop Quantum Gravity, you wouldn’t find smooth, continuous space. Instead, you’d discover something resembling a vast three-dimensional spider web—a network of quantum threads connecting tiny volumes of space, each thread carrying discrete units of area, each junction containing quantized volumes.

This is the world of spin networks, where space itself becomes granular, atomic, and fundamentally discrete. But why should we believe such an exotic picture? The answer lies in one of physics’ most pressing crises: the seemingly impossible task of reconciling Einstein’s general relativity with quantum mechanics. Today, we’ll explore how spin networks emerged as a potential solution, what they tell us about black holes and the Big Bang, and why they might represent the true quantum nature of spacetime itself.

The Fundamental Crisis: When Einstein Meets Heisenberg

The crisis at the heart of modern physics stems from a fundamental incompatibility between our two most successful theories. On one side stands general relativity, Einstein’s geometric theory of gravity, which describes spacetime as a smooth, continuous manifold that curves in response to matter and energy:

\[R_{\mu\nu} - \frac{1}{2}Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}\]

Here, the left side describes the curvature of spacetime (with $R_{\mu\nu}$ being the Ricci curvature tensor and $g_{\mu\nu}$ the metric), while the right side represents matter and energy (through the stress-energy tensor $T_{\mu\nu}$). This elegant equation has explained everything from planetary orbits to gravitational waves, treating spacetime as an infinitely divisible continuum.

On the other side stands quantum mechanics, where physical quantities come in discrete packets and uncertainty reigns supreme. The evolution of quantum systems follows the Schrödinger equation:

\[i\hbar\frac{\partial \psi}{\partial t} = \hat{H}\psi\]

where $\psi$ is the wave function and $\hat{H}$ is the Hamiltonian operator. Unlike general relativity’s deterministic geometry, quantum mechanics is inherently probabilistic and operates against a fixed background spacetime.

The trouble arises when we try to unite these frameworks. Consider what happens near a black hole’s center or during the first moments of the Big Bang. Here, quantum effects become important precisely where spacetime curvature becomes extreme. We need a theory that treats both gravity and quantum mechanics on equal footing—a theory of quantum gravity.

Standard approaches to quantizing gravity run into severe mathematical difficulties. When physicists try to apply quantum field theory techniques to gravity, they encounter non-renormalizable infinities. The perturbative expansion of the metric $g_{\mu\nu} = \eta_{\mu\nu} + \kappa h_{\mu\nu}$ (where $\eta_{\mu\nu}$ is flat spacetime, $h_{\mu\nu}$ represents gravitational waves, and $\kappa = \sqrt{32\pi G}$ sets the coupling strength) requires an infinite number of parameters to absorb divergences—a sign that the theory is fundamentally incomplete.

More fundamentally, there’s a conceptual problem: in quantum field theory, particles interact against a fixed background spacetime, but in general relativity, spacetime itself is dynamical. There is no fixed background—the stage and the actors are one and the same.

This is where Loop Quantum Gravity enters the picture, offering a radically different approach that takes general relativity’s background independence seriously while embracing quantum mechanics’ discrete nature.

The Revolutionary Framework: From Connections to Quantum Geometry

Loop Quantum Gravity began with a crucial insight by Abhay Ashtekar in the 1980s: instead of trying to quantize the metric tensor directly, we can reformulate general relativity using variables that more closely resemble those of successful quantum field theories like electromagnetism.

Ashtekar introduced new variables to describe the gravitational field:

• A connection field $A_a^i(x)$, similar to the electromagnetic vector potential
• A densitized triad field $E^a_i(x)$, related to the spatial geometry

These variables satisfy the fundamental Poisson bracket relation:

\[\{A_a^i(x), E^b_j(y)\} = \kappa \delta_a^b \delta^i_j \delta^3(x-y)\]

where $\kappa$ is a coupling constant and $\delta$ symbols ensure the variables at different points don’t interact classically.

The beauty of this reformulation becomes apparent when we examine the constraints that govern general relativity in this language. The theory must satisfy three types of constraints:

1. Gauss constraint: $\mathcal{G}_i = D_a E^a_i = 0$, ensuring gauge invariance
2. Diffeomorphism constraint: \(\mathcal{C}_a = E^{b}_{i} F_{ab}^{i} = 0\), preserving spatial coordinate freedom
3. Hamiltonian constraint: $\mathcal{H} = \epsilon_{ijk}E^a_i E^b_j F_{ab}^k + \cdots = 0$, governing time evolution

Here, $F_{ab}^i = \partial_a A_b^i - \partial_b A_a^i + \epsilon^i_{jk}A_a^j A_b^k$ is the curvature of the connection, analogous to the electromagnetic field strength.

The quantum theory emerges by promoting these classical variables to operators acting on quantum states. But what are these quantum states? This is where spin networks make their dramatic entrance.

Instead of working with the connection field $A_a^i(x)$ directly (which would be mathematically intractable), we consider its holonomies—path-ordered exponentials along curves $\gamma$:

\[h_\gamma[A] = \mathcal{P}\exp\left(\int_\gamma A_a^i \tau_i dx^a\right)\]

where $\tau_i$ are Pauli matrices and $\mathcal{P}$ denotes path ordering. These holonomies have a crucial property: they’re gauge-invariant and well-defined even in the quantum theory.

Similarly, instead of the electric field $E^a_i(x)$, we work with flux variables through surfaces $S$:

\[E_S(f) = \int_S E^a_i f^i n_a d^2x\]

where $f^i$ is a test function and $n_a$ is the surface normal.

The quantum states of geometry are then built from these holonomies and fluxes, leading naturally to spin network states—quantum superpositions of discrete geometric configurations.

Spin Networks: The Atoms of Space

A spin network is essentially a graph embedded in three-dimensional space, but it’s a very special kind of graph. Each edge carries a label $j = 0, \frac{1}{2}, 1, \frac{3}{2}, 2, \ldots$ corresponding to irreducible representations of the SU(2) group—the same group that governs quantum mechanical spin. Each vertex where edges meet contains an “intertwiner,” a mathematical object that ensures the overall state respects gauge invariance.

Formally, a spin network state is written as:

\[|\Gamma, \{j_e\}, \{i_v\}\rangle\]

where $\Gamma$ is the graph, ${j_e}$ are the spin labels on edges $e$, and ${i_v}$ are intertwiners at vertices $v$.

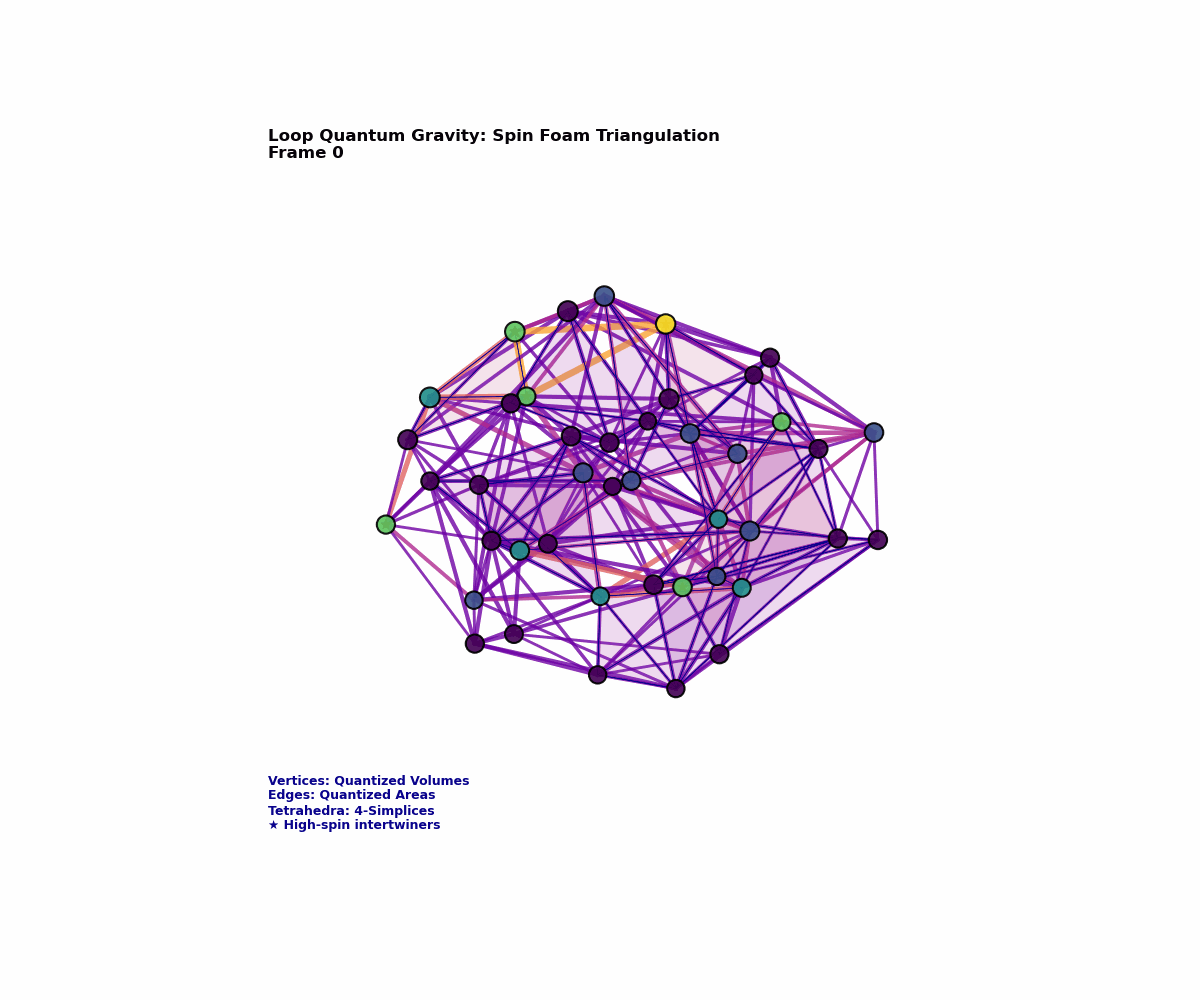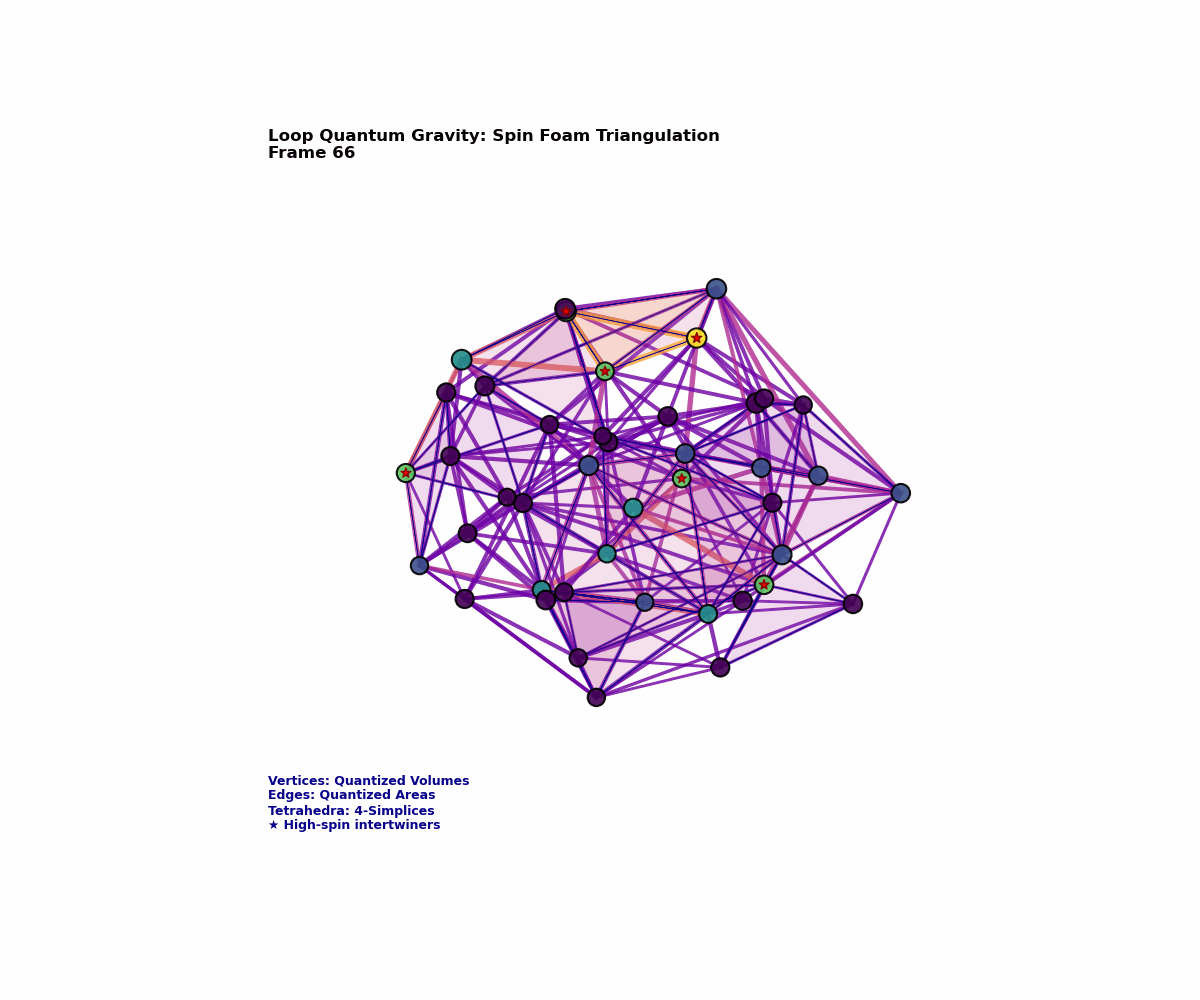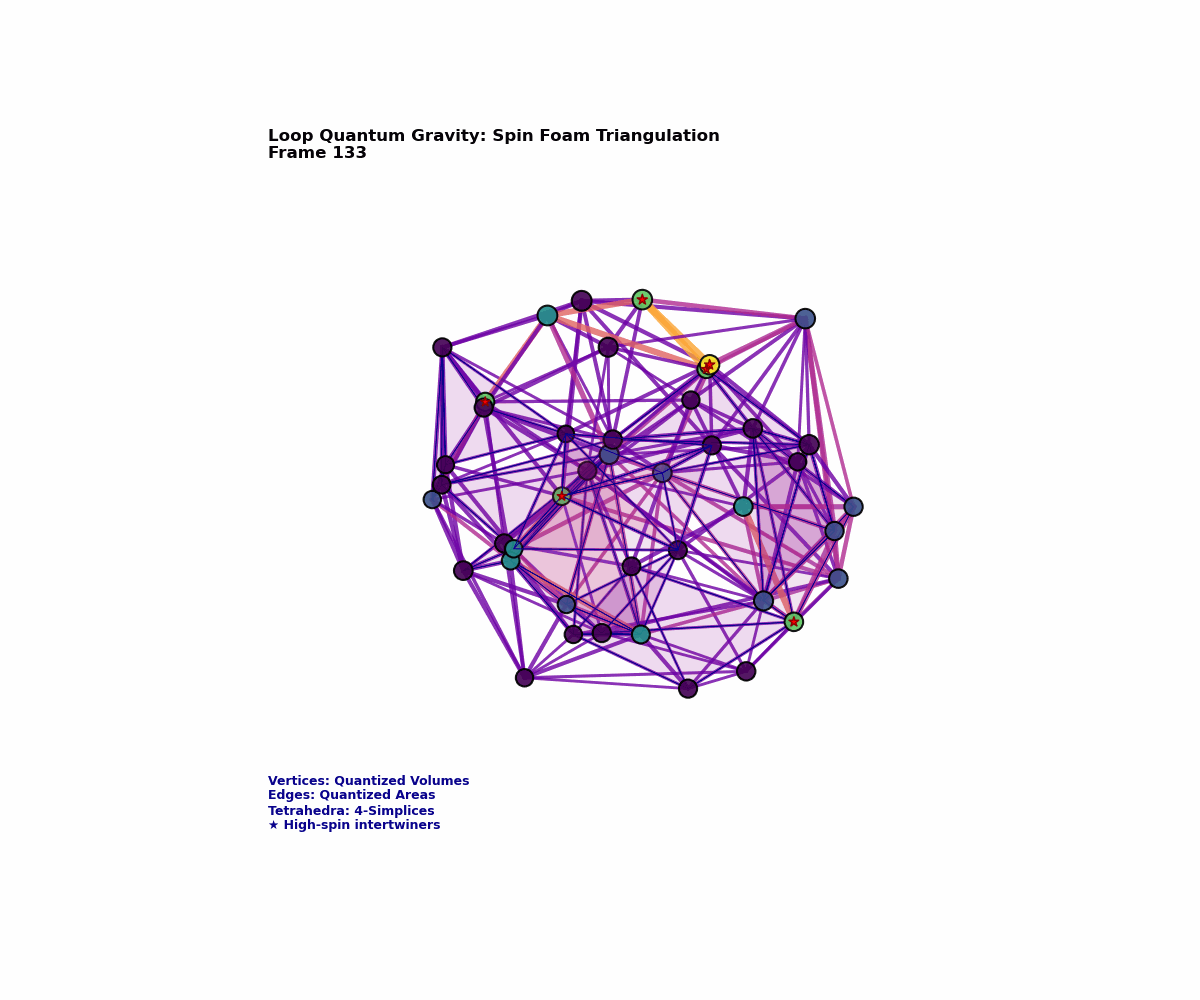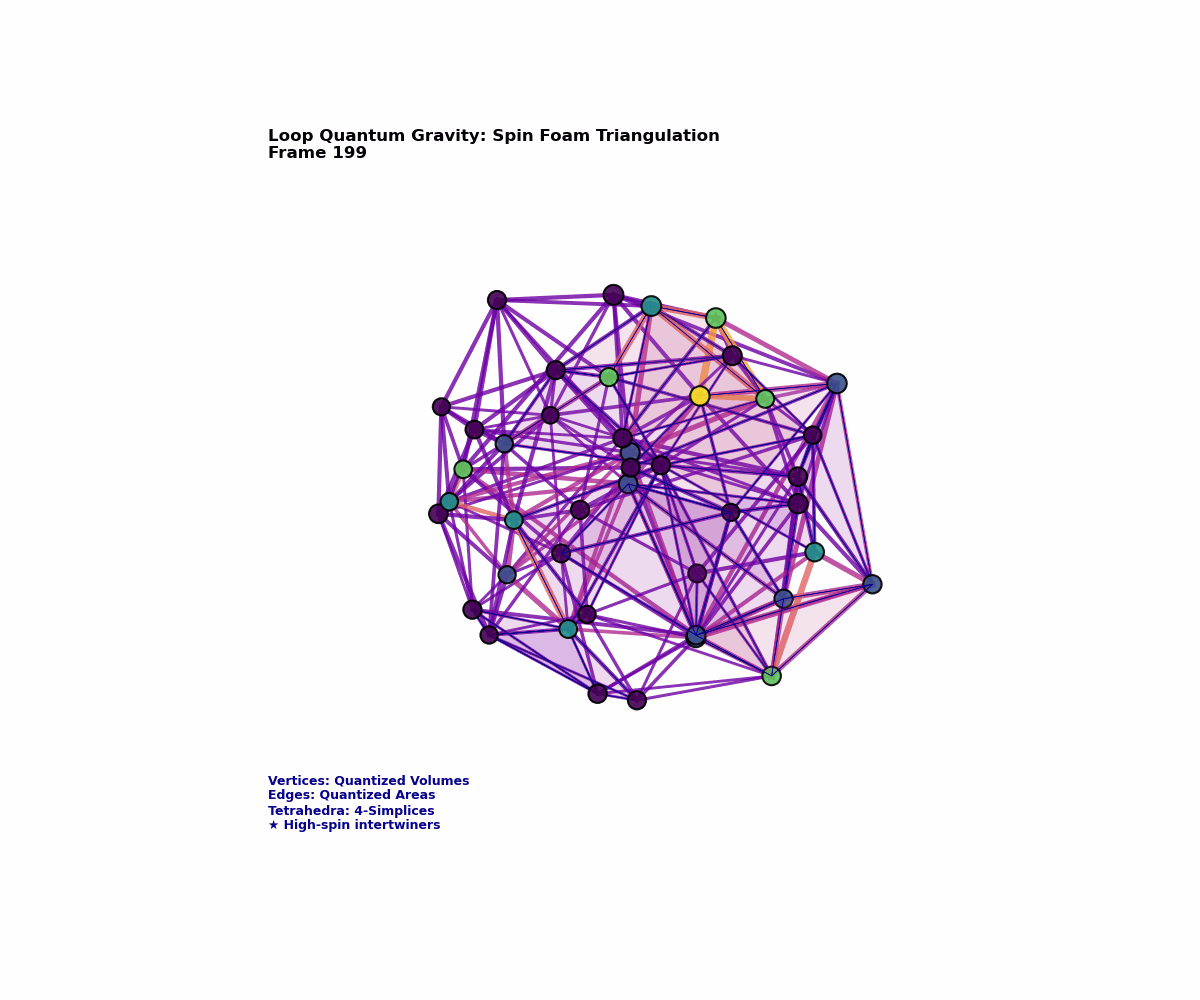
What makes spin networks remarkable is their direct geometric interpretation. Each edge carrying spin $j$ represents a quantum of area:

\[A_{\text{edge}} = 8\pi\gamma\ell_P^2 \sqrt{j(j+1)}\]

where $\gamma$ is the Immirzi parameter (approximately 0.24) and $\ell_P = \sqrt{\hbar G/c^3}$ is the Planck length. This means that area—one of the most basic geometric quantities—is quantized at the Planck scale.

Similarly, each vertex represents a quantum of volume, though the volume formula is more complex:

\[V_{\text{vertex}} = \ell_P^3 \sqrt{\left|\frac{1}{8}\sum_{I,J,K} \epsilon_{ijk} \epsilon^{IJK} J^i_I J^j_J J^k_K\right|}\]

where the sum runs over edges meeting at the vertex, and $J^i_I$ are angular momentum operators.

This leads to a startling conclusion: space itself has an atomic structure. Just as matter is composed of discrete atoms rather than being infinitely divisible, space consists of discrete quanta connected by discrete relationships. The smooth spacetime of our everyday experience emerges only as a statistical average over enormous numbers of these quantum geometric degrees of freedom.

To understand how this works, consider an analogy with fluid mechanics. Water appears continuous and smooth at large scales, but zoom in far enough and you discover it’s made of discrete molecules. The smooth flow of water emerges from the collective behavior of countless molecules, each following quantum mechanical rules. Similarly, smooth spacetime emerges from the collective behavior of countless spin network nodes and edges, each carrying discrete quanta of area and volume.

The Quantum Resolution of Spacetime Singularities

One of the most compelling features of spin networks is their potential to resolve the singularity problems that plague classical general relativity. In Einstein’s theory, certain situations—like black hole centers and the Big Bang—lead to infinite densities and curvatures, points where the theory breaks down completely.

Consider a black hole described by the Schwarzschild metric:

\[ds^2 = -\left(1-\frac{2GM}{r}\right)dt^2 + \left(1-\frac{2GM}{r}\right)^{-1}dr^2 + r^2d\Omega^2\]

This develops a singularity at $r = 0$ where the curvature scalar $R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma} \sim r^{-6}$ diverges. Physically, this suggests infinite tidal forces and energy densities—clearly unphysical.

In Loop Quantum Gravity, however, the discrete structure of space prevents such infinities. As matter collapses, it cannot be compressed beyond a certain quantum geometric limit set by the minimum possible volume of a spin network vertex. Instead of forming a singularity, the matter reaches a maximum density of approximately:

\[\rho_{\max} \sim \frac{c^5}{\hbar G^2} \approx 5 \times 10^{96} \text{ kg/m}^3\]

This is enormous—about $10^{77}$ times the density of an atomic nucleus—but finite. The black hole’s interior becomes a quantum geometric structure with discrete, finite properties.

Even more dramatically, Loop Quantum Cosmology—the application of spin network techniques to the entire universe—suggests that the Big Bang singularity is replaced by a “Big Bounce.” The modified Friedmann equation becomes:

\[H^2 = \frac{8\pi G}{3}\rho\left(1-\frac{\rho}{\rho_c}\right)\]

where $H$ is the Hubble parameter, $\rho$ is the energy density, and $\rho_c \approx 0.41 \rho_{\text{Planck}}$ is a critical density. When $\rho$ approaches $\rho_c$, the expansion rate $H$ goes to zero and then becomes negative—the universe bounces from a previous contracting phase into our current expanding phase.

This suggests our universe might be just one cycle in an eternal series of expansions and contractions, with quantum geometry preventing the formation of a true beginning or end.

Experimental Challenges and Future Prospects

Testing quantum gravity presents extraordinary challenges. The characteristic energy scale where quantum gravitational effects become important is the Planck energy:

\[E_{\text{Planck}} = \sqrt{\frac{\hbar c^5}{G}} \approx 1.22 \times 10^{19} \text{ GeV}\]

This is about $10^{16}$ times higher than the energies achieved in the Large Hadron Collider—far beyond any conceivable particle accelerator.

However, several potential windows for observation exist. The discrete structure of spacetime might leave subtle signatures in cosmological observations. The primordial power spectrum of density fluctuations could be modified, changing the cosmic microwave background in detectable ways. The scalar spectral index $n_s$ and tensor-to-scalar ratio $r$ might deviate from standard inflation predictions:

\(n_s = 1 - 6\epsilon + 2\eta + \delta_{\text{LQG}}\) \(r = 16\epsilon \cdot \xi_{\text{LQG}}\)

where $\delta_{\text{LQG}}$ and $\xi_{\text{LQG}}$ encode quantum geometric corrections.

Another possibility involves high-energy astrophysics. If spacetime is discrete, photon propagation might be slightly modified at extreme energies:

\[E^2 = p^2c^2 + m^2c^4 + \alpha \frac{E^3}{E_{\text{Planck}}}\]

This could cause high-energy photons from gamma-ray bursts to arrive slightly later than low-energy ones, potentially observable with sensitive timing measurements.

Black hole physics offers another testing ground. The Bekenstein-Hawking entropy formula receives quantum corrections in LQG:

\[S_{\text{BH}} = \frac{A}{4\ell_P^2} - \frac{1}{2}\ln\left(\frac{A}{\ell_P^2}\right) + \mathcal{O}(1)\]

The logarithmic correction term might be detectable in gravitational wave observations of black hole mergers, though this remains challenging with current technology.

Despite these possibilities, significant theoretical challenges remain. The dynamics of spin networks—how they evolve in time—is still not fully understood. Various proposals exist for the quantum Hamiltonian constraint:

\[\hat{\mathcal{H}} = \sum_v \hat{\mathcal{H}}_v\]

where $\hat{\mathcal{H}}_v$ acts at each vertex, but the precise form remains controversial. Different choices lead to potentially different physical predictions, making the theory’s completion urgent.

Perhaps most importantly, demonstrating that general relativity emerges from spin networks in the appropriate classical limit remains challenging. Semiclassical states must satisfy:

\[\langle\hat{O}\rangle_{\text{semiclassical}} \approx O_{\text{classical}} + \mathcal{O}(\hbar)\]

for all relevant observables $\hat{O}$, but proving this rigorously for the full theory is an ongoing research program.

The Deeper Implications: Reality as Quantum Information

Spin networks suggest a profound reconceptualization of space, time, and matter. In the traditional view, space provides a passive stage upon which matter and energy interact. Spin networks flip this picture: space itself becomes an active, dynamical entity with quantum properties.

The mathematical structure underlying spin networks connects to deep areas of pure mathematics. Spin networks are essentially morphisms in the category of SU(2) representations, connecting them to knot theory, topology, and quantum information theory. The evaluation of a closed spin network (one with no open edges) yields topological invariants related to knot polynomials:

\[\langle K \rangle = \sum_{\{j_e\}} \prod_e (-1)^{2j_e}(2j_e+1) \text{ev}(K_{\{j_e\}})\]

where $\text{ev}(K_{{j_e}})$ is the evaluation of the spin network obtained by decorating knot $K$ with spins ${j_e}$.

This suggests deep connections between quantum gravity and quantum information. Area and volume operators fail to commute:

\([\hat{A}(S_1), \hat{A}(S_2)] \neq 0 \text{ if } S_1 \cap S_2 \neq \emptyset\) \([\hat{V}(R), \hat{A}(S)] \neq 0 \text{ if } S \cap R \neq \emptyset\)

This non-commutativity implies fundamental uncertainty relations for geometry itself—we cannot simultaneously measure the areas of overlapping surfaces or the volume and area of intersecting regions with perfect precision.

In this picture, spacetime emerges from more fundamental quantum information-theoretic structures. The classical notion of locality—that distant events cannot influence each other instantaneously—becomes approximate, valid only for coarse-grained descriptions that average over many quantum geometric degrees of freedom.

Some researchers speculate that spin networks might provide insights into the holographic principle and the AdS/CFT correspondence, suggesting that all the information in a volume of space can be encoded on its boundary. If so, the quantum geometry described by spin networks might be dual to some boundary quantum field theory, opening new avenues for understanding both quantum gravity and many-body quantum systems.

Whether spin networks ultimately prove correct or represent stepping stones toward a more complete theory, they have already transformed how we think about space, time, and the quantum nature of reality. They suggest that the smooth spacetime of our experience emerges from an underlying discrete quantum geometry—a web of relationships that constitutes the most fundamental level of physical reality.

In weaving together the insights of general relativity and quantum mechanics, spin networks offer not just a mathematical framework but a new vision of the cosmos: one where space and time themselves are quantum mechanical, where the universe computes its own evolution through discrete geometric relationships, and where the fabric of reality is quite literally woven from quantum threads of area and volume.

The implications extend far beyond theoretical physics. If spacetime is indeed quantized, it suggests deep connections between gravity, quantum computation, and information theory. The universe might be performing a vast quantum computation, with spin networks as its basic computational elements and the laws of physics as its programming.

Whether this vision proves correct awaits future theoretical developments and experimental observations. But already, spin networks have given us a new language for describing reality at its most fundamental level—a language in which space, time, matter, and information merge into a unified quantum geometric framework that might finally reconcile Einstein’s vision of curved spacetime with Heisenberg’s quantum uncertainty.