Introduction

Last week I came across a fascinating research paper, “Tail Protection for Long Investors: Trend Convexity at Work” by researchers from Capital Fund Management. As someone who’s weathered multiple market cycles, I’ve always been intrigued by investment strategies that can protect portfolios during turbulent times. The 2008 financial crisis and the March 2020 COVID crash demonstrated just how quickly markets can unravel, leaving many investors scrambling for protection.

Most long-term investors face a common dilemma: how to maintain exposure to market growth while protecting against significant downturns. Traditional approaches like diversification often fail during crises when correlations spike. Buying put options works but comes at a steep cost that erodes returns over time. This is where trend following strategies reveal their hidden superpower—convexity.

What Makes Trend Following Special?

Unlike typical hedge fund strategies that often disappoint during market crashes (showing negative convexity), trend following strategies have historically performed better during periods of high volatility. Look at the performance of Commodity Trading Advisors (CTAs) during the 2008 Lehman crisis—they delivered strong positive returns while markets collapsed.

This distinctive behavior makes trend strategies a potentially valuable addition to long-only portfolios. But what drives this performance? The researchers explain it through a surprisingly elegant mathematical relationship. The performance of trend following can be understood as the difference between long-term variance and short-term variance.

The Mathematics Behind the Magic

For those who enjoy the technical details, here’s the core insight: If we define a simple trend strategy where the positino \(\Pi\) at time \(t\) is proportional to the price difference:

\[\Pi_t := \lambda A_t \left(S_t - S_{0}\right)\]

where \(\lambda\) is a scaling factor and \(A_t\) is the capital engaged (set to 1 for simplicity). The profit and loss (PnL) from \(t-1\) to \(t\) becomes:

\[G_t:= \Pi_{t-1} D_t = \lambda D_t \sum_{t'=1}^{t-1} D_{t'}\]

where \(D_t\) is the price changes from \(t-1\) to \(t\). Aggregating this over \(T\) over \(T\) days and rearranging the sums:

\[G_t = \frac{\lambda}{2} \left(S_T - S_0 \right)^2 - \frac{\lambda}{2} \sum_{t=1}^{T} D_t^2\]

This means the strategy’s average aggregated performance equals:

\[\left\langle \sum_{t=1}^{T}G_t \right\rangle = \frac{\lambda T}{2}\left(\sigma^2(T) - \sigma^2(1)\right)\]

In plain English: trend following strategies swap short-term volatility for long-term volatility. When markets make large moves over extended periods, these strategies shine. This creates a natural convexity in the performance profile - the strategy performs increasingly better as market volatility increases.

I’ve found this insight particularly valuable in my own investing. During calm markets, trend following often underperforms or generates modest returns. But when markets experience extended turbulence, these strategies can deliver outsized performance that helps offset losses in traditional investments.

Understanding Different Trend Implementations

The beauty of the researchers’ findings is that this relationship holds true across various trend implementations. Whether using exponential moving averages (EMAs), position capping, or different signal processing methods, the core mathematical relationship remains.

For example, using a classic EMA-based trend strategy where:

\[\Pi_t := \frac{\lambda_{\tau} L_{\tau}[R_t]}{\sigma_t}\]

Where \(L_{\tau}\) represents an EMA with timescale \(\tau\) and \(R_t\) are the returns normalized by volatility. The performance still captures the spread between long-term and short-term volatility:

\[L_{\tau '} [G_t] = \frac{\lambda \tau}{\tau -1} \left( \tau L^2_{\tau} [R_t] - L_{\tau '} [R_t^2] \right)\]

When I first implemented trend strategies in my portfolio, I spent endless hours optimizing parameters without fully understanding these mathematical foundations. Knowing the underlying mechanics now helps me focus on what matters - ensuring my trend system captures the right time horizon for the risks I’m trying to hedge.

Time Horizons: The Critical Factor

One crucial insight that changed my approach to trend following is understanding the importance of time horizons. A trend strategy with a 6-month lookback window provides protection against large market moves that unfold over several months—not against overnight crashes or flash crashes.

The paper elaborates on this by showing how the strategy’s convexity is most visible when performance is measured over the appropriate timeframe. Using a 180-day trend filter, the researchers demonstrated that aggregating performance over approximately 90 days reveals much stronger convexity than what appears in daily or monthly returns.

This explains why many investors miss the protective benefits of trend following—they’re looking at returns on the wrong timeframe. During the COVID crash, for instance, many trend followers initially lost money in the sudden selloff, only to recover and profit as the trend established itself over subsequent weeks.

Real-World Applications: CTA Performance

Commodity Trading Advisors (CTAs) are the most prominent practitioners of trend following strategies. The authors analyzed the SG CTA Index, demonstrating that their simple trend model achieved over 80% correlation with the index by using just a handful of liquid futures markets and a basic trend signal.

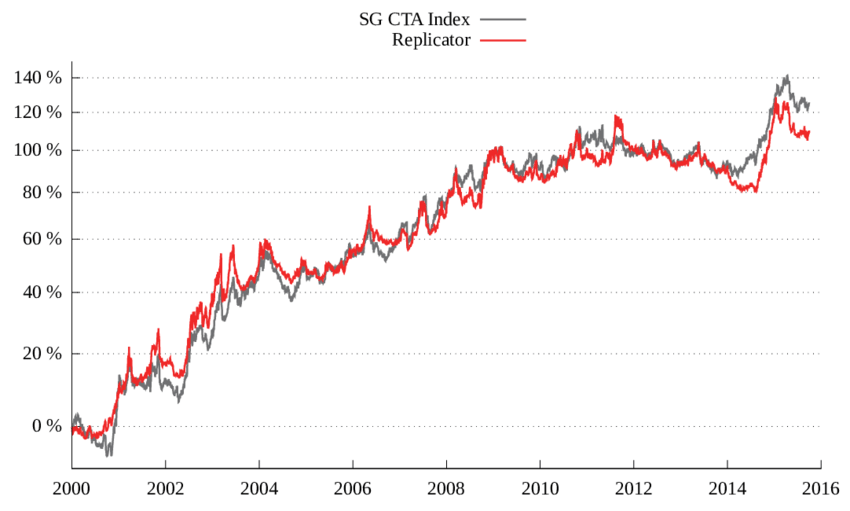SG CTA index replication through simple trend model

What struck me most was how they revealed the convexity of CTA performance. By appropriately measuring over the right timeframe (approximately 6 months for the trend and 3 months for performance aggregation), they showed much stronger convexity than previously observed. The R-squared of the quadratic fit increased from a mere 0.02 in naïve analysis to a more convincing 0.2 using their methodology.

Diversification Effects: Single-Asset vs Multi-Asset Trend

The research also revealed an important nuance—diversification reduces convexity. A single-asset trend following strategy shows stronger convexity than a diversified portfolio of trend strategies.

However, diversified trend strategies still offer significant protection to diversified long portfolios. The authors demonstrated a mathematical relationship showing that trend strategies provide effective hedging for Risk Parity portfolios in particular. This makes intuitive sense to me, as Risk Parity strategies already balance risk across asset classes, and trend strategies can adapt to trends in any of those same asset classes.

In my experience, this creates a natural complementarity. When rising interest rates hurt both stocks and bonds in 2022, for instance, trend strategies were able to capture the downtrends across multiple assets, providing valuable protection to traditional portfolios.

Trend Following vs. Options: A Cost-Effective Alternative

Many investors turn to options for portfolio protection. While buying index puts provides guaranteed protection, they typically come with a high price tag that erodes long-term returns.

The research highlights how trend following offers similar convexity benefits but at a lower cost. Their analysis showed that a portfolio of strangle options provides exposure to long-term variance similar to trend following strategies. The key difference? Options have a fixed entry cost (the premium), while trend strategies pay with realized short-term volatility.

The researchers demonstrate this with a fascinating relationship. A properly constructed strangle portfolio’s P&L can be expressed as:

\[G_{T}^{\text{strangles}} := \frac{1}{2} \left( S_{T} - S_0 \right)^2 - T \bar{\sigma}^2_{0,T}\]

where \(\bar{\sigma}^2_{0,T}\) is an effective implied volatility. Compare this to the trend following P&L:

\[G_T := \frac{\lambda}{2} \left( S_{T} - S_0 \right)^2 - \frac{\lambda}{2} \sum_{t=1}^{T} D_t^2\]

Both strategies provide exposure to \((S_T - S_0)^2\) (long-term variance), but at different costs. Since options are typically sold at a premium, trend following offers a more economical approach to convexity over time.

This makes trend following a more cost-effective hedge over the long run, as demonstrated by their positive long-term performance compared to consistently losing money with long-option portfolios.

Practical Implementation Considerations

If you’re considering adding trend following to your portfolio, here are some practical considerations I’ve learned through experience:

1. Time horizon matching: Choose trend parameters that align with the market risks you’re trying to hedge. Short-term traders need faster signals, while long-term investors can use longer lookback periods.
2. Position sizing: Proper risk scaling is essential. Too little exposure won’t provide meaningful protection, while too much introduces its own risks.
3. Multiple timeframes: Consider using trend signals across multiple timeframes to capture different market regimes.
4. Transaction costs: Factor in trading costs, which can significantly impact performance, especially for shorter-term implementations.
5. Tax efficiency: In taxable accounts, trend strategies may generate more frequent trading and short-term capital gains.

My Key Takeaways

After studying this paper and implementing trend strategies in my own portfolio, I’ve drawn three important conclusions for investors:

1. Time horizon matters: Trend strategies protect against large moves over their specific time horizon. A 6-month trend strategy won’t help with overnight crashes.
2. Diversification reduces convexity: Single-asset trend strategies show stronger convexity than diversified ones, but diversification brings other benefits like smoother returns.
3. Risk parity complement: Trend following strategies offer excellent protection for risk parity portfolios, making them valuable for investors with diversified long positions across equities and bonds.

Final Thoughts

What fascinated me most about this research is how it quantifies what many trend followers have intuitively understood. These strategies offer affordable downside protection without sacrificing long-term returns, making them uniquely valuable in an investment landscape dominated by high correlation during crises.

The elegant mathematics behind trend following—swapping short-term variance for long-term variance—explains why these strategies have persisted as effective tools for centuries despite being well-known market anomalies.

For long-term investors, adding a trend component to your portfolio might be worth considering—especially if you’re concerned about preserving capital during extended market downturns. Whether implementing a simple moving average crossover system or a more sophisticated ensemble approach, the core mathematical benefits remain.

As markets continue to evolve, trend following strategies offer a robust approach to protection that doesn’t rely on forecasting or timing market tops—just systematically adapting to changing conditions as they unfold.

---

Have you incorporated trend following strategies in your portfolio? Share your experience in the comments below. What timeframes have you found most effective for your investment goals?

Keywords: trend following strategies, portfolio protection, market volatility, CTA performance, risk management, convexity, long-term investing, tail risk, risk parity, options alternatives